Major flaw in Theory of Relativity

Relativity of simultaneity shows flaw when a third simultaneous even is introduced in the "Ladder Paradox" thought experiment.
Link to the Wikipedia page, treating the ladder paradox - click HERE to read.
Please study the content from the above link, and refer to it when examining the problem presented by me.
For better understanding I'll use the same graphics, modified for the purpose of the problem.
To question the length contraction and the relativity of simultaneity I introduce a third simultaneous event in the ladder paradox problem.
How? Simply, by attaching a rod to each door, which are welded perpendicularly on the inside of the doors, in a way that the rod tips touch when both the doors are closed. (See the red attached arms on the graphics)
Think of this touching event as verification of the simultaneity - touching verifies simultaneity, no touching - no simultaneity. Obviously this event will be absent in the ladder reference frame, since the doors in that frame are not closing simultaneously. Missing event in one of the reference frames is against the law of physics, which automatically puts Einstein's Theory of Relativity in the dustbin. (Don't laugh. Think.)
Graphics:
1. left hand side - garage reference frame with simultaneously closing doors. Touching event is present on the third graphic from the top.
2. right hand side - ladder reference frame with non simultaneously closing doors. Touching event is missing.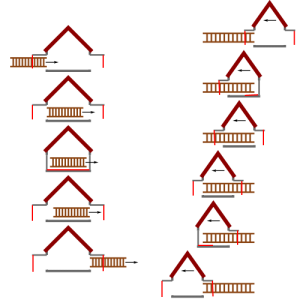
Why do I present this problem in your forums?
Just to show, how authorities create unbreakable walls and form mind obedience.
You are terrified by the idea of Einstein being wrong in the core of his theory, eh?
No, you are not. You cannot even allow such a thought in your obedient minds.
You think that I'm crazy, and that solves all your problems with all your wrong perceptions of the world.
- Login to post comments

I have been at online debate on several websites for the past 15 years and see the same tactics from EVERY major religion in the world. I've seen not only Christians, but Muslims and Jews and Hindus and Buddhists try to debunk science, then when they cant do that, they attempt to co opt science to point to their club. It doesn't work when any of you try it.
Debunking science is only done through testing and falsification and peer review. Doing that does not magically make Jesus or Allah or Yahweh or Vishnu or Buddha the gatekeepers of truth. Scientific method is a tool, not a religion. It is completely religion independent and does not prop up the bible, Quran, Torah or Talmud, or the Baghavad Gita or Buddha or book of Moromon or Shinto religions.
This is simply crap you attempt like every other religion becuase the fear of being finite is too scary to you. Too bad, your baggage, not ours.
"We are a nation of Christians and Muslims, Jews and Hindus -- and nonbelievers."Obama
Check out my poetry here on Rational Responders Like my poetry thread on Facebook under Brian James Rational Poet, @Brianrrs37 on Twitter and my blog at www.brianjamesrationalpoet.blog
I find it highly amusing that Brian can't even solve the simplest logical puzzle put forward by a theist who simply doesn't understand physics.
This experiment fails because absolute simultaneity is impossible. The front of the ladder might enter the garage and stop suddenly, but the back of the ladder will keep moving until the force of the stop traverses the entire ladder. If the ladder made it into the garage simultaneously, it would instantly snap or shatter. Which means it never made it inside the garage in one piece in the first place. Which means relativity is correct.
Enlightened Atheist, Gaming God.
you haven't seen a hindu or buddhist do any such a thing because you haven't ever said jack motherfucking squat to a hindu or buddhist.
"I have never felt comfortable around people who talk about their feelings for Jesus, or any other deity for that matter, because they are usually none too bright. . . . Or maybe 'stupid' is a better way of saying it; but I have never seen much point in getting heavy with either stupid people or Jesus freaks, just as long as they don't bother me. In a world as weird and cruel as this one we have made for ourselves, I figure anybody who can find peace and personal happiness without ripping off somebody else deserves to be left alone. They will not inherit the earth, but then neither will I. . . . And I have learned to live, as it were, with the idea that I will never find peace and happiness, either. But as long as I know there's a pretty good chance I can get my hands on either one of them every once in a while, I do the best I can between high spots."
--Hunter S. Thompson
https://sites.google.com/site/oldseers.
Study how religion is relative to nonsense. Come back in 6 months.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
@Brian, where did you see me talking about religion!?
Can you comment on the experiment or not?
@Vastet, there is no such think as "absosulte simultaneity". It is either simultaneous or not.
The ladder cannot get into the garage "simultaneously". Simultaneity does not apply to the ladder but to the opening and closing of the doors.
The ladder never stops in the garage. Where did you get that idea from?
And guys, do not be in a hurry to judge other people scientific knowledge, before you get yours knowledge straight.
@Old Seer, are you talking to me!?
I'm not familiar with the problem. I just woke up and blurted--I thought this was something else. I tried to retract--but to late.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
These types of problems come about becasue the observer may be unfamilliar with all the ins and outs and overlook a detail. It very likely is a problem that requires one to see two things at the same time which cannot always be done. . I doubt that relativity will ever be found false.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
This demonstrates a lack of comprehension. The doors are irrelevant, except in that they enforce a space in which the ladder cannot fit. You might be able to get the ladder in regardless, but due to the fact it cannot fit if the doors are closed simultaneously, the ladder will shatter the instant it is confined in the garage. The very plank second it is contained in the garage in its entirety, it will cease to be a ladder, therefore you never contain the ladder in the garage.
If the ladder never stops, then the ladder is never entirely confined within the garage. You can put cameras on either end of the ladder and demonstrate that at no time are both ends of the ladder are in the garage.
No matter what you do, the ladder is never completely within the garage.
Enlightened Atheist, Gaming God.
So, I also haven't been and ancient Egyptian polytheist, or a Greek or Roman polytheist, still does not make any god real or any religion a requirement for evolution to occur. You've seen every post I've made ever on every page on social media so you should know right?
"We are a nation of Christians and Muslims, Jews and Hindus -- and nonbelievers."Obama
Check out my poetry here on Rational Responders Like my poetry thread on Facebook under Brian James Rational Poet, @Brianrrs37 on Twitter and my blog at www.brianjamesrationalpoet.blog
I also cant build a car factory to build a car from scratch, but it doesn't take a rocket scientist to know cars don't run on sky wizards. You keep missing the point it doesn't matter which person of any religion starts bringing science into it, they all fail.
If he were making this argument to prove the existence of Allah you wouldn't buy it. If he were making this argument to prove the existence of Yahweh you wouldn't buy it. If he were making the argument for Vishnu you also wouldn't buy it.
"We are a nation of Christians and Muslims, Jews and Hindus -- and nonbelievers."Obama
Check out my poetry here on Rational Responders Like my poetry thread on Facebook under Brian James Rational Poet, @Brianrrs37 on Twitter and my blog at www.brianjamesrationalpoet.blog
Yes, it is bullshit because your goal is to say "I'm right, now here is where I fill in the gap with my personal pet sky wizard claim".
How about you cut to the chase. Do you have evidence for the god you believe is real?
"We are a nation of Christians and Muslims, Jews and Hindus -- and nonbelievers."Obama
Check out my poetry here on Rational Responders Like my poetry thread on Facebook under Brian James Rational Poet, @Brianrrs37 on Twitter and my blog at www.brianjamesrationalpoet.blog
You are just proving my point; your mind was molded by authorities, to the point that you are afraid to utter the truth which your eyes are seeing.
You don't believe in yourself, because Einstein taught you that you should trust him more than you trust your own intelligence.
In fact it is not Einstein who taught you so. It is the society which put Einstein on pedestal and presented him to you as an unqestionable genius.
I am giving you the proof that relativity is false. Why don't you accept it?
I'll tell you why; because to you I'm not an authority. The truth which I'm telling you, no matter how obvious it is, must come to you from higher place, and only then you'll accept it.
Religion vs science/physics, or what?
Vastet, the doors are not irrelevant and that's the whole point; having relativity of simultaneity. In one frame of reference you have simultaneously closing doors and in the other have no simultaneity.
There is no place for argument whether the ladder stops in the garage or not - it doesn't stop in both frames of reference, but that's not the point and it does not affect the outcome of my experiment.
It is as simple as it gets; in the garage frame of reference we can verify simultaneity with the touching event of the two rod tips.
In the ladder reference frame, we cannot verify simultaneity, because according to STR, longer ladder passes through shorter garage due to the relativity of simultaneity.
Hence one event is missing, which makes relativity false.
It is as simple as that, and it doesn't leave place for arguments.
You are to much obsessed with "God who does not exist" and cannot see what I'm trying to tell you.
I'm not talking about God here. I'm trying to tell you how you see and how you "know" your surrounding.
Actually I'm telling you that most people don't have their own knowledge and opinion.
Most people are like parrots who repeat the knowledge they were taught by authorities.
Man vs truth.
I gave you irrefutable proof that relativity is false.
How do you deal with that truth?
should be in the irrationalities thread.
You're guessing.
Im a physicist but I'm not a Einstien freak. He's been found wrong on several things, he's not infalliable. The Old Seers reject the concept of authority, so we're not puppets to anyone.
I don't reject you information. At this point I don't understand it. You may be right. Did you look up all concerning informataion, or is this your own.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
I'm glad that you are one of the few who leaves some room for doubts.
Yet, you are considering my statement as "information".
It is not an "information". It is a statement supported with proof.
Again, you are afraid to speak up your mind, because "how could I go against such an authority as Einstein" and all the guild of scientists who already accepted STR as core theory in physics...
I personally came up with the presented problem, and brought it to the attention of many physicists.
Have to say that most of them preferred to humiliate themselves with childish arguments, rather than accepting the obvious truth.
Of course I didn't expect something else. Such behavior is normal for 99% of humans.
Brian keeps missing the point that he's always wrong about everything, and always will be, unless he actually learns to shut his fool mouth and learn.
In this topic, for example, religion was never even mentioned until Brian showed up. A purely scientific statement was made (wrongly, but still). Then Brian comes in screaming about religion because he's really a theist and can't stand the idea that religion has nothing to do with the topic.
Enlightened Atheist, Gaming God.
Wrong.
Impossible. No two objects can have the exact same perspective without holding the exact same position at the exact same time, which is not possible.
Irrelevant. Whether the doors close or not, the ladder is never completely within the garage. The doors do not matter.
Nope.
You don't seem to understand that relativity is relative.If you're on the ladder, the garage appears smaller, but it isn't. And if you're in the garage, the ladder appears shorter. But it isn't.
You don't know shit about relativity.
Enlightened Atheist, Gaming God.
If there is no such thing as relativity then your post is irrelevent. I don't get it.
If you're demontrating that societies are made up via authorities--I agree. We're on the same page there. That's what The Old Seers are all about.
Considering that your label here is "theist" then you are also under some type of authority, would that not be correct. You'll notice that mine here is also under theist, but I'm not the one that attached the label--I just live with it.
Relativity (if I got it right) is the study of how things in the universe are related and under what forces. Or, the laws of physics are the same everywhere. BUT- there is evidence that at some point in partical physics, certain observable facts break down, such as, there are particlas that can be in different places at the same time. Maybe this is what you're dealing with. BUT (again) PRACTICAL Physics that we use in everyday life remains relative to life. If you're dealing with the speed of light --be aware that it's a field that is still under study, and at this time the info isn't avaiable to show you to be right or wrong. You may be under the idea that all is known when it isn't.
How can your post be relative to anything if there's no relativity. That means my post has no relativity either.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
Einstien has no authority in my life what-so ever. I decide. He has presentations that I have yet to work on "if" it interests me. There-fore I have to exclude myself from seeing your post as right or wrong. This reminds me of the problem of (which is a different case of course) how long does it take a train 1 mile long to go through a tunnel one mlie long at 60 miles an hour.
Be aware, that Einstirn had troubles tieing his shoes. Appaently it was to simple for him to understake. Be careful with the phenomenon of truth.
Originally I didn't understand your post. I took it as a Thesist vs science. I woke up from a nap and as usual for the first few minutes I'm in two or more universes and have to take time to figure out which one I'm in. Had I taken time to look it over I very likely wouldn't have commented. There are floks here that are much more up on this facet of phisics then I. If you consult with anyone here you will find without a doubt that I am deffinetly not afraid to be wrong.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
if i claim to have spoken to a certain type of person, yet consistently get EVERYTHING about that type of person wrong, any intelligent person is going to reach the conclusion that i am lying about having talked to that type of person. it's called inference, and almost every system of logic in the world accepts it as a valid source of knowledge.
and you ARE lying: you have just admitted, in your typically oblique, cowardly way, that you have never spoken directly to a hindu or buddhist. yet in a previous post, you claimed to have "debated" them. unless you were talking about debating imaginary hindus and buddhists in your own head, that was obviously a lie. you are a liar. of course, everyone here already knew that.
"I have never felt comfortable around people who talk about their feelings for Jesus, or any other deity for that matter, because they are usually none too bright. . . . Or maybe 'stupid' is a better way of saying it; but I have never seen much point in getting heavy with either stupid people or Jesus freaks, just as long as they don't bother me. In a world as weird and cruel as this one we have made for ourselves, I figure anybody who can find peace and personal happiness without ripping off somebody else deserves to be left alone. They will not inherit the earth, but then neither will I. . . . And I have learned to live, as it were, with the idea that I will never find peace and happiness, either. But as long as I know there's a pretty good chance I can get my hands on either one of them every once in a while, I do the best I can between high spots."
--Hunter S. Thompson
@Vastet, please do not try to guess what I know about relativity, and just follow the prbolem as presented in the OP.
Study the matter from Wikipedia (link is provided) if you didn't study it in the school.
Try to at least stay in the already accepted by the science scenario in the ladder-paradox problem.
Of course the ladder is completely within the garage in the garage frame of reference (left graphics, third image from the top).
In the ladder reference frame it is never completely within the garage, because in that frame it is longer than the garage, hence the need for relativity of simultaneity.
However, a simple addition to the experiment (a third simultaneous event) shows the weak point of the whole theory.
By the way, do you have anything to do with physics?
@Old Seer, my point is, that one cannot come to any truth before he/she overthrows all knowledge molded in his mind by authorities.
A very simple experiment shows the fallacy of Einstein's "genius" mind, but who is brave enough to acknowledge it?
And before you are ready to see the obvious truth like the one I gave you in the OP, you'll never be ready to know the truth about God.
Now, I see that you are theist, Old Seer, but as long as you know God from the books and from the words of authorities, you'll never know the Real God, and you do not have the right to argue about God's existence, unless you were personally touched by the power called God.
There are so many different churches in the world, and all of them are preaching different God, with different rules, and different rewards.
No wonder that the atheist are growing in numbers.
So, again back to my point; a man have to be free minded and brave enough to meet the truth.
How can one accept the idea of God, if cannot accept the very obvious idea of Einstein being wrong?
But wait, Einstein has nothing to do with all this matter. It is the ego that stays on people's way.
You denounce Einstein - you denounce your knowledge, you denounce yourself. And who does that? Fools. But only fools, empty from any knowledge can "see" God.
As I can understand from dealing with past Theists, you have to start over from square one, which I doubt you'll do. Go over all the definitions, claims, and insights in the use of the term, "God". and see what you find.
Go to the site previous mentioned and start over. I have plenty of posts here on the subject you'll very likely deny to be true. You investigate (if you do) at your own paril. Be advised, we do not debate, discuss, argue or get into verbal shootouts. There-fore, form lessons learned by me trying to be helpful to no effect, you're on your own, as Theists tend to give me bible lessons I don't need. Whatever you find don't tell me about it--I already know what you'll find. If you wish to argue any of the information presented by us take it to a clergyman--he'll deny everything, it's his job on the line, not ours. Lets see if you take or use your own advice. You're right on the free mind, lets see how free your mind is. So, start looking amd see if you can find you. Good hunting.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
Old Seer, never make assumptions about people you've just met, and you'll never be wrong.
I'm not going to flood you with Bible quotations, neither am I going to advocate for any religion.
I'm not a religious man, I don't go to church and I don't preach God known from books and scriptures.
If you feel insecure around me, don't worry, I promise, I'll behave
OK, lets put it this way then. To understand us you'll need to look over what we see. Go to the website and see what you find. Don't believe us, make up your own mind. I understand you very well. You seem to be a good candidate for understanding. We present what we find is true, you have to decide what is true or false for yourself.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
Thank you Old Seer, I'll have all that in mind.
By the way, this forum is not new to me.
I'm registered member since 2008 and I know some of the rationalists here.
I believe they remember me too.
You are fairly religious neutral, you shouldn't have any problem understanding us. The others were the same. I was Atheist since 1962 to 1964 or in that time span. I didn't take it seriously until the Seers formed. Some of them were members of small churches, probably country sized. Even as Atheistic it still took a while for me to get used to the idea there was no spy in the sky. Old mental habits take a while to change. This may not be the place to be touching tootsies. There is the conversations forum where I have Old Seers Corner, or for Araujo. Any conversations should be posted there. I'm glad to make your Acquaintence.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
Relativity tells us that the concept of simultaneosness is not valid. But then this supposed paradox uses simultaneousness to try disproved Relativity. So your so called paradox is actually argument for Relativity.
Circular reasoning, isn't circular reasoning the classic argument of thiests?
thedragoninmygarage.tumblr.com/post/36514225579/circular-reasoning-also-known-as-paradoxical
Taxation is the price we pay for failing to build a civilized society. The higher the tax level, the greater the failure. A centrally planned totalitarian state represents a complete defeat for the civilized world, while a totally voluntary society represents its ultimate success. --Mark Skousen
The fact you think you've demonstrated a flaw in the theory of relativity with this bullshit proves absolutely that you know shit about relativity. I don't need to guess. It's a fact you just demonstrated to anyone who cares to look.
Take your own advice.
Look who's talking.
Which is an illusion that only works on one end of the garage at a time. Put cameras at both ends and you won't catch a moment when the ladder is completely in the garage. The actual dimensions on objects don't change, they only appear to change. All your bullshit about doors and third simultaneous events are just bullshit from a mind that doesn't comprehend how it works. You could have a billion simultaneous events and it wouldn't mean squat. They all have their own relativity.They all have their own perceptions. But it doesn't have any impact on the actual positions of objects.
Furthermore, this isn't even an experiment, because you have no way to actually test this out. In comparison to dozens of tests that have supported relativity, including the web of satellites in orbit right now that depend on relativity to provide GPS coordinates. Coordinates that work despite your egotistical claim that it doesn't because of a ladder and a garage.
Next thing you'll tell me is that evolution doesn't happen because there are still apes and the moon landing was faked because the Earth is flat. And you can prove it with a thought experiment. And I'll tell you to stay in philosophy and leave science to the scientists.
Enlightened Atheist, Gaming God.
please don't foist him on us. after eight years on this site, i've had enough of philosophy being a fucking whipping-boy.
"I have never felt comfortable around people who talk about their feelings for Jesus, or any other deity for that matter, because they are usually none too bright. . . . Or maybe 'stupid' is a better way of saying it; but I have never seen much point in getting heavy with either stupid people or Jesus freaks, just as long as they don't bother me. In a world as weird and cruel as this one we have made for ourselves, I figure anybody who can find peace and personal happiness without ripping off somebody else deserves to be left alone. They will not inherit the earth, but then neither will I. . . . And I have learned to live, as it were, with the idea that I will never find peace and happiness, either. But as long as I know there's a pretty good chance I can get my hands on either one of them every once in a while, I do the best I can between high spots."
--Hunter S. Thompson
Relativity doesn't tell us that the concept of simultaneity is not valid. What do you mean by "not valid"(!)
Relativity simply states that there could be simultaneity in one frame of reference while not having it in another reference frame.
I'm arguing that statement and proving it wrong.
Vastet, I'll restrain from answering in your manner.
Argumentum ad hominem does not add any weight to your comments.
The ladder paradox is a thought experiment which explains relativity of simultaneity, and is widely accepted by the scientific community.
Adding one more event to that experiment makes it invalid as supportive proof for the relativity of simultaneity.
I expected some of you to come up with the GPS system, and there you are
Well, that calculations do not work 100%. They are approximate and have to be corrected from time to time.
Same calculations could be done without using relativity and GPS system would still work.
I haven't even begun to insult you. Keep lying, however, and that will change very quickly.
YOUR ladder "thought experiment" is not widely accepted by the scientific community because it is bullshit. The paradox in this is an illusion. As stated by the very article you linked to. As stated by the theory of relativity itself. Learn what 'appears' means, specifically in scientific literature.
No, adding one more event merely adds one more perception with its own relativity.
Yeah, because all the satellites and the Earth are moving. Kind of throws a wrench in long term scenarios. Kind of like how every 4 years enough extra seconds add up to make a 29th of February.
No, it wouldn't. It would never work. Every single second that went by would have the coordinates off by more than the previous second. Time is affecting those satellites at a different rate than it affects us.
Like I said: you don't know shit about relativity.
Enlightened Atheist, Gaming God.
OK, Vastet. Lets do it your way.
Using moronic language and attitude is not my cup of tea but for you, I'll try my best.
First of all my clever boy, thought experiments are used by science in many occasions to prove a point.
The ladder paradox experiment came as prove that relativity works.
How?
I'll explain it for you, and you promise to remember it, and not make fool of yourself in front of intelligent people.
So, read carefully.
The question was: if length contraction works, then a longer ladder should be able to shrink enough to go through shorter garage with simultaneously shutting doors.
Yes, was the answer, it will go through the garage.
But - was the argument - from the ladder reference frame, the garage will look even shorter. How the ladder could fit in it?
Oh, you don't take in account the relativity of simultaneity, was the clever answer.
Let me show you how is done, continued the clever guy.
In the garage frame of reference, the ladder is contracted and of course it will fit in the garage between the simultaneously closed doors.
That may look very difficult to you, but with good maths and speed synchronization, theoretically and even in practice it could be done.
(Note that since this is thought experiment, we don't care about the speed of the closing and opening doors, as long as they are bellow the speed of light. Of course we still don't have the technology for such doors, but AGAIN, this is a thought experiment. Read in Wikipedia what "thought experiment" is.)
So, in the garage reference frame we encounter simultaneously closing and opening doors, and all goes well with the ladder passing through.
Now we go to the ladder reference frame.
Hm, well, here is different scenario. The ladder sees the garage approaching in very high speed, which contracts its length, and makes it even shorter that it already is.
How to pass through, thinks the ladder? Of course, the answer is in the laws of relativity.
When the doors are opened, the ladder speeds in the garage and just before to arrive to the exit door, sees the door shutting close and open immediately. But that's not the case with the entry door, which is still opened, waiting for the rear of the ladder to pass through. Why is that? because according to relativity, the order of the events depends on their proximity to the observer in relation to the direction of movement(this explanation is especially for slow minds to be able to visualize the scenario). So the exit door is closer in the direction of movement and it closes first, and then immediately opens, which gives way for the ladder to exit with its front part, and get in the garage with its rear part. Right after the rear of the ladder enters the garage, the entry door closes and opens again. The ladder speeds out of the garage and that's it. Relativity is proven along with the length contraction.
BUT, it appears that Einstein did not see a small problem. Such scenario allows for an event to go missing, which is against the basic laws of physics.
With my addition I'm showing how that touching event goes missing in the ladder reference frame.
That is more than enough to debunk a theory.
It doesn't matter whether the experiment can be done in reality.
It shows the theoretical impossibility of relativity.
So, now Vastet, do you understand what am I talking about, or will you go in further self humiliation and disgrace?
You've demonstrated nothing BUT a moronic attitude and language since you started posting.
I'll note also that you were the first to bring in the term moronic, so look in the mirror if you want to cry about name calling.
No. No thought experiment has ever been considered proof, or disproof, of a theory. You need an actual, material, reproducible experiment. The very fact that you and I see different results from your experiment conclusively proves the conclusion you came to is unreproducible. Making it useless.
I'd tell you to follow your own advice, but it's way too late for that.
YOU still fail to appreciate the difference between appear and is. The ladder might appear to be within the garage from a specific reference point, but it never actually is in the garage. No matter what you do to measure the objects, you will never find a point where the ladder actually is completely in the garage. Never.
As your entire argument is based on this failure to comprehend relativity, your entire argument is bullshit.
Thank you come again.
Enlightened Atheist, Gaming God.
You obviously have absolutelly wrong conception about realtivity, Vastetd.
There is no "appear" in that game. The things are as they are in each frame of reference. The garage has no other reference but its own and same goes for the ladder.
The garage measures a short ladder approaching it with the attempt to pass through and that it what it is - short ladder passing through simultaneously shutting doors. Hence the presence of simultaneity in the garage frame of reference.
The ladder measures short garage approaching it, and that's what it deals with - short garage.
You have to understand that, because this is the whole point of relativity.
holy shit, it's neil young!
Since touching is dependant on simultanity, touching would seem to appear in one frame of reference but not another.
You're trying to tell us that simultaneousness depends on FoR, but touching ia independent of FoR. This is irrational.
Taxation is the price we pay for failing to build a civilized society. The higher the tax level, the greater the failure. A centrally planned totalitarian state represents a complete defeat for the civilized world, while a totally voluntary society represents its ultimate success. --Mark Skousen
I finally got around to looking at this.
https://www.youtube.com/watch?v=wteiuxyqtoM
Having given this some thought it turns out I am familiar with this problem, but have nothing definete that I can make ouit. In a certain level of my past physics the problem was presented useing a space craft rather then a train.
Problem #1- our ancesters developed the hatchet. Before the invention of the hatchet was there ever a hatchet before the first one.
OK, so lets say that before there were any cognative beings to make a hatchet, a rock tumbles down the mountain and strikes another breaking off pieces. One of the pieces is shaped like a hatchet. Question. Does then, the universe contain a hatchet.
What must be taken into account is, what happens when intellect becomes present in the universe.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
Says the person unqualified to make such a comment, who has demonstrated multiple times that you don't know shit about relativity.
Yes there is.
Wrong. The garage has a frame of reference; the ladder. The garage is positioned relative to the ladder, and vice versa.
Cameras placed at both doors prove that is an illusion, and if the doors ever close with the ladder partially contained within then the ladder ceases to exist.
No.
No.
No.
Enlightened Atheist, Gaming God.
Simultaneity does not depend on the frame of reference. It depends on the time the events happen.
If the events happen in the same time, then they are simultaneous.
Is what you're getting at- when a 3rd item enters the problem is when simulaiety breaks down?
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth
Vastet, if I continue this discussion with you, I'll make fool of myself.
You have no clue about General and Special Relativity.
Let me give you one:
You keep throwing the "appear" word in the context of relativity.
"Appear" implies perception.
However relativity is not about perception but about measured values.
When we measure length in inertial frames of reference, we get true values, not perceived, imaginary values.
If we measure 1m length, it is 1m long and we can use that 1m long object by putting it to work in a system as 1m long object.
Same goes for simultaneity. If the events happen at the same time, then they are simultaneous. If they don't happen at the same time, then they are not simultaneous.
I cannot explain it in more simple way.
When and if you comprehend the above, you'll be able to get a grasp of the problem I presented in the OP.
Being arrogant, clueless bully doesn't make you right, my boy. I'll scratch you off the list of the "rationalresponders", until you show some understanding on the subject.
Not third item, but third event.
And no, the third event does not brake the simultaneity. The "rod touching event" (third event) is present in the garage frame, where simultaneity exist, and is missing in the ladder frame of reference, where simultaneity does not exist.
The problem is that while we can have diferent order of the events in the diferent frames of referenc, we cannot have missing event in one of them. That would be against the law of physics.
The only possible thing the world needs saving from are those running it.
https://sites.google.com/site/oldseers
Knowledge trumps faith and I'm not a Theist
Lies are nothing more then falsehoods searching for the truth